Angora: Efficient Fuzzing by Principled Search
0x00 解决路径问题的五种技术
-
上下文敏感路径覆盖 (像AFL这种都是基于bitmap的edge计数,并不细分edge的上下文)
-
关于taint analysis 确定 input 和 path constraints之间的映射。
-
梯度下降算法 作用在 input mutate(ion)
-
input的结构推导 (shape => 结构, type => 结构里面字段)
-
input长度的探索方法
0x01 Something interesting
上下文分支敏感的分支统计
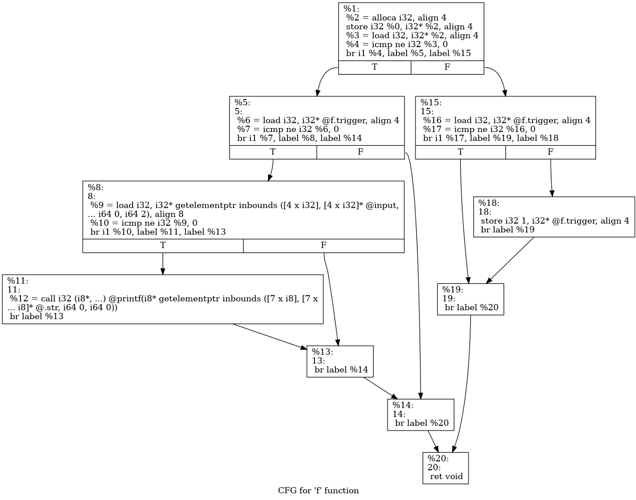
通常情况下我们的分支记录在有向图CFG上来完成,通过执行过程中对经过有向边edge进行计数,这里会丢失一些东西,理想情况下,在CFG上记录一条完整的分支,应该是edges的一个拓扑排序 (e_1,e_2,\ldots,e_n) ,这里变成了单纯的edge计数。作者并没有对这里进行改进,同样还是edge计数,但是他们把相同的edge,置于不同的上下文当作两个不同的edge,这里的上下文特指执行当前edge的函数调用栈。这样在原来计数的基础上提出了更细的计数对象,在一定程度能更细致的区别执行过程中edge的变化。(这些理解只看原文,其实有一点难理解,需要具体的看一下Angora中LLVM Pass过程)
文章在这里用一个例子说明问题,但是这个例子我觉得并不好,作者认为原有的edge计数并不能区别输入为10和01的区别,实际上是可以区别的:
10: L3:true;L4:false;L3:false;L10:true;
01: L3:false:L10:true;L3:true:L4:true;L5:(true|false);
两次执行走的分支情况,在01下是其实触发了新的路径,会多出一个L5分支记录,原文说两次都触发执行了L4,L10会被认为没有触发新路径。但是01的时候是触发了L5。
注意label %5这个基本块,01是会触发label %5到label %8这条边的。所以这个例子实际上在这里不合适。那在这里什么样的例子应该合适呢?应该是确保走过相同的edge的,不同上下文带来的影响。我能想到的唯一改变是下列这种情况:
void f(int x){
...
}
void main(){
if(input()=='111'){
f(input());
f(input());
}
}
加入context以后,因为L7和L8,处于不同callside,但是两者调用f,假设经过的edge一样,会导致在f,会多出一倍的edge元素,就像我前面说的,可能以前某个edge计数为2,可能现在被拆分成了两个不同的edge。在某种程度上改变了AFL中的edge计数的feature,可能变得更“敏感”一些了。但是我很难去推演它的这种”敏感“,到底能带来什么?我想要知道这种形式的”敏感“,是否可以孤身存在,而不对其他东西产生影响?这些东西于我而言,现在还是难以解释。
字节粒度的污点分析 (没有涉及taint rules)
文中没有细讲taint的过程,而是主要讲了一下taint过程中的污点表示,taint存在的意义是为了将输入和路径条件建立映射关系,在mutating阶段能更好的去解决路径条件。
定义:标签 t_x 表示输入input中的哪些字节会流入变量 x 。通常 t_x 用位向量来表示, t_x 会随着输入的大小线性增长。为了应对large input,文中构造了一个数据结构,来存储和查询 t_x :
-
Binary tree:( b 代表一个位向量, |b| 代表位向量的长度,长度概念应用树里面,就是指结点的高度)每一个位向量 b ,都可以用这个树上的高度为 |b| 的节点 v_b 唯一表示,从根节点root到 v_b 路径上的节点依次展开为 b_0,b1,\ldots 。其中的每个结点都一个指向它父结点的指针,这样可以从 v_b 开始顺着树回溯遍历得到完整 b 。
-
Look-up table: 表里存储着 t_x \rightarrow v_b , 即保存着指向 Binary tree里面结点的指针。
画了一个图,方便理解和记忆:
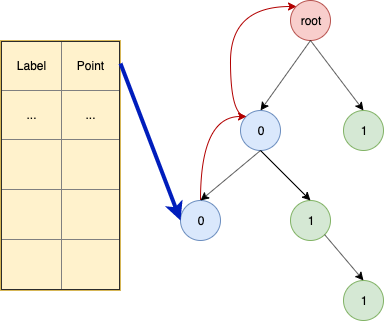
t_x 插入操作:
1. 去掉 v_b 结尾所有的0。
2. 遵循Binary tree策略,用 b 去遍历Binary tree,如果 b_i=0 ,则follow左子结点,反之亦然,如果子结点不存在则创建结点。
3. 把 t_x 存储到树上最后一个visited的结点。
注意到这个算法只在生产新结点的时候,插入 t_x ,所以某个结点如果存在 t_x 则后面都是不会发生改变的。我计算得到的空间复杂度跟原文有一定区别,原文是 O(l*logl) ,我在计算最坏复杂度时得到的是 O(nl-l*logl) .
Maybe i am wrong,who know!
基于梯度下降的搜索算法
目标是解决路径,让路径条件满足某种要求,我们从最简单的条件出发,某个二元运算,和两个基本变量:我用 \odot 泛指所有可能出现的二元运算,基本变量用 a , b 表示:
文中尝试将求解约束转化成最优化问题,所以需要让上面的问号变成一个具体的值,而不是通常情况下的 \{0,1 \} ,文中做一个漂亮的转换。
将二元运算转化成了具体函数,函数值间接表示约束的成立。通过合适的函数表示,将所有的约束成立都变成了 f(x) \le 0 ,复杂的组合条件可以经过转换变成简单的二元运算:
if(a&b){}
//transform
if(a){
if(b){
}
}
这样,向最优化问题的转换变成了可能。注意 f 实际上还是一个黑盒函数,你是并不知道它完整构造的,只能通过输入,得到输出,也是一个无约束最优化的标准问题,为了解决这个问题,文中使用梯度下降的方法。
使用梯度下降过程中需要计算梯度,但是前面说了这里的 f 是一个完全黑盒的函数,甚至可能都不是一个连续的函数。在没有其他方法的情况,只能通过近似计算梯度,来保证后面的运算。
现给出 f 的定义: f(\mathbf{X}) ,其中 \mathbf{X}=(x_1,\ldots,x_i) ,即输入input中与f对应二元运算相关联的值。注意这里的 x_i 并不完全是像 b 中的 b_i 一样是单个字节,后面还有一个结构感知的过程,这里 x_i 可能是一个完整类型的变量。对于多元函数 f(\mathbf{X}) 而言,它的梯度定义为:
其中
\delta 是一个极小的正数(e.g. ,1), v_i 表示 i 方向上的单位向量。为了计算每个方向上的偏导数,需要跑两次input,第一次使用original input ,第二次使用经过变换preturbed input X+\delta v_i ,这里有一个非常重要的问题,有可能第二次使用preturbed input的时候,导致 f 所指的二元运算所在程序位置变成了unreachable,这个时候会导致无法计算或者计算出来的结果是毫无意义的。原文在这里没有细谈,而是一笔带过,但是在Matryoshka中在这里提到一种解决方法,有兴趣的同学可以去看看。
f(\mathbf{X}) 最后是否能收敛到理想状态的下(小于0或者小于等于0) ,文中提到了三个点:
- f(\mathbf{X}) 是一个单调函数或者凸函数。
- 局部最小值满足约束。
- 如果局部最小值不满足于约束,Angora将会随机的使用其他的 \mathbf{X}' ,直到局部最小值满足约束。
结构和类型推断
前面提到过 f(\mathbf{X}) 中的 \mathbf{X} 并不是完全字节粒度的位向量,Angora会尝试把一起使用的字节归纳为一个type。文中这里也提到了一个问题,关于为什么要引入这个机制?假设某个程序把4个连续的字节 b_3b_2b_1b_0 当作一个int类型,用 x_i 代表这个整型,那么在计算 f(\mathbf{X}+\delta v_i) 的时候,只需要在 x_i 加上 \delta ,但是把其分开成4个方向偏导数分别计算,可能会影响其收敛速度。
结构推断:哪些bytes总是一起被使用?
类型推断:一起被使用bytes是什么类型?
Angora里面的primitive type分为1,2,4,8bytes。它们之前可能会出现矛盾情况(e.g. 相同连续位置,被fetch一次8bytes,同时也被fetch一次4bytes),这种情况下,取最短的type。类型推断的依据使用其上下文的语义所决定的,比如某个指令操作对象是signed int,那么对应的type也是signed int。注意其整个过程都是在动态的污点分析中完成的。
输入长度探索
Angora这里特别地采取了关于输入长度的判断策略,通过关联read-like函数和read 系统调用,对read-like函数传参判定对应的输入offset(taint相关), 还会特殊标记它们的返回值,如果它们的返回值流到了路径条件上,且没有满足路径条件,Angora会尝试增加输入长度。这里我觉得这个策略并不会普遍适用于一般的程序输入,只能说一种有趣的尝试。
0x02 Self Conclusion
很有趣且朴素的一篇文章,使用的5种解决路径方法很实用,且开源(能看代码的感觉真好),但是仔细研究细节可能还是与自己想的不太一样。其中很多东西,可以尝试应用到实际情况下,我觉得就值得。“纸上得来终觉浅,绝知此事要躬行”。